Everything You Need to Know about Immediate Inferences
Categorical
statements always begin with one of the following three quantifiers: “all”, “no”, or “some”.
The
subject and predicate terms must be general
terms, i.e., plural nouns or noun
phrases. The letters “S” and “P” should
be understood to indicate the terms in the subject (“S”) and predicate (“P”)
positions in the statement.
The
verb is always the same: “are”, understood in the copulative sense of the verb “to be”.
The
word “not” appears in the O proposition only, after the copula.
There
are four categorical statement forms, as shown in the table below.
|
Form |
Name |
Quantity |
Quality |
Distribution
of S term |
Distribution
of P term |
|
All
Ss are Ps |
A |
Universal |
Affirmative |
Distributed |
Undistributed |
|
No
Ss are Ps |
E |
Universal |
Negative |
Distributed |
Distributed |
|
Some
Ss are Ps |
I |
Particular |
Affirmative |
Undistributed |
Undistributed |
|
Some
Ss are not Ps |
O |
Particular |
Negative |
Undistributed |
Distributed |
(“All
Ss are not Ps” is syntactically ambiguous and therefore not a categorical statement form.)
The
affirmative categoricals (A and I) are named from the Latin word “affirmo”.
The
negative categoricals (E and O) are named from the Latin word “nego”.
A
term is distributed in a categorical
if the statement says something about all
the members of the class denoted by the term. The attributes of the “S” term
(e.g., the subject term is distributed in the A statement) apply to whatever term is in the subject
position; for example, if you flipped the subject and predicate terms, then “P”
would be in the subject position and would therefore be distributed.
Mnemonics
for remembering distribution: (1)
“AsEbInOp”; (2) “Any student earning Bs is not on probation”; (3) Universals (A
and E) distribute subjects; negatives (E and O) distribute predicates.
Aristotelian and Boolean
Interpretations
The
universals are A (“All Ss are Ps”) and E (“No Ss are Ps”). The interpretation of universals is different
in the traditional (Aristotelian) and modern (Boolean) approaches.
The
Aristotelian interpretation of A is “If anything is an S, it’s a P; and Ss
exist.”
The
Aristotelian interpretation of E is “If anything is an S, it isn’t a P; and Ss
exist.”
The
Boolean (modern) interpretation of A is “If anything is an S, it’s a P”. Period.
We don’t assume Ss exist.
The
Boolean (modern) interpretation of E is “If anything is an S, it’s not a
P.” Period. We don’t assume Ss exist.
The
particulars are I (“Some Ss are Ps”) and O “Some Ss are not Ps”). The particulars have the same meaning in both
the Aristotelian and Boolean interpretations.
Both I and O make existence claims, and thus have metaphysical as well
as logical import.
The
I statement means “At least one thing exists that is both S and P”.
The
O statement says “At least one thing exists that is S and not P.”
Both
interpretations (Aristotelian and Boolean) of the universals (A and E) have
their advantages. People do mostly talk
about existing things, so the Aristotelian approach captures that. The Aristotelian approach allows you to infer
I from A; that is, if the premise “All Ss are Ps” is true, it follows that
“Some Ss are Ps”. This inference is called subalternation.
Usually there’s no problem with that: people would agree that if it’s true that
all apples are fruit, it must be true that some apples are fruit. But note that the I proposition is always
understood to make an existence claim. “Some apples are fruit” means “There
exists at least one thing that is both an apple and a fruit.” And that’s fine as long as apples exist in
the first place.
Since
the Aristotelian approach assumes Ss exist, it is impossible (on the
Aristotelian interpretation) for both I and O to be false; one or the other or
both must be true. If at least one S
exists, it’s either in P or it’s not; it can’t be in neither. This is called the subcontrary relationship between I and O.
Also,
since the Aristotelian approach assumes Ss exist, then if A is true, E is
necessarily false; and if E is true, A is necessarily false. For example, if WVC students exist, then if
it’s true that “All WVC students are human” it must be false that “No WVC
students are human”. This is called the contrary
relationship between A and E.
The
down side of the Aristotelian approach is that people don’t always talk about
things that exist. For example, the A
statement “All unicorns are one-horned animals” has a non-denoting term
(“unicorns”) as subject. In that case,
you wouldn’t want to allow the subalternation inference from A to I, since the
existence claim in the I statement would be false: it’s false that there exists
at least one thing that is both a unicorn and a one-horned animal. Furthermore, if Ss don’t exist, you wouldn’t
want to say that if A is true, E must be false (the contrary relation). On the Aristotelian interpretation, you’d
have to say that if “All unicorns are one-horned animals” is true, then “No
unicorns are one-horned animals” must be false.
That seems wrong, since if unicorns don’t exist in the first place, the
statement “No unicorns are one-horned animals” seems just as true as “All
unicorns are one-horned animals”.
The
advantage of the Boolean approach is that it’s more general, allowing logic to
handle arguments that deal with non-existent Ss. The Boolean approach does not allow the
subalternation inference from A to I, nor does it allow the contrary
relationship between A and E, nor the subcontrary relationship between I and
O. If Ss don’t exist, then A does not
imply I nor does E imply O. If Ss don’t
exist, both I and E could be false. If
Ss don’t exist, then both A and E could be true.
Venn Diagrams
In
Venn diagrams, each term gets a circle.
Each categorical statement contains two terms, S and P. So we begin with two intersecting
circles.
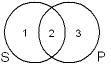
Area
1 is the area of things that are S but not P.
Area
2 is the area of things that are both S and P.
Area
3 is the area of things that are P but not S.
Area
4 (everything outside the intersecting circles) is everything else.
How
to mark a Venn diagram:
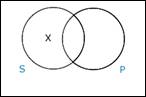
1. Shade an
area: means the area is empty (has no
members)
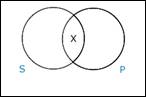
2. Uncircled X in
an area: means the area is non-empty (has at least one member) in both
traditional and Boolean interpretations
3. Circled X in an
area: means the area is non-empty in the traditional interpretation only
4. No mark in
area: not enough information to say whether this area has members or not
Traditional (Aristotelian) Universals
Trad
A: If anything is S, it’s P; and Ss
exist. Trad
E: If anything is S, it’s not P, and
Ss exist.
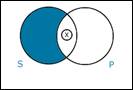
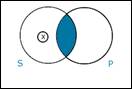
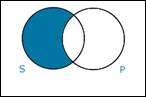
Modern
(Boolean) Universals
Modern A: If anything is S, it’s P. Modern E:
If anything is S, it’s not P.

Particulars
– same in Aristotelian and Boolean interpretations
I: Something exists that is both S
and P. O: Something exists that is both S and
not P.
Contradictories
Two
statements are contradictories of each other if they always have opposite truth
values, i.e.,
·
if
one is true, the other is false
AND
·
If
one is false, the other is true.
In
categorical logic, the pairs of contradictories are
A
and O
and
E
and I.
These
pairs of statements are contradictory in both the Boolean (modern) or
Aristotelian (traditional) interpretations of the universals. In fact, the Boolean square of opposition
(below) contains only the
contradictories.
Using
Venn diagrams, you can see why A and O are contradictory: If A is true (in
either the Boolean or Aristotelian interpretations), area 1 is shaded (i.e.,
empty). But in O, area 1 has an X (i.e., not empty). Since area 1 is either empty or not, one or
the other, A or O, must be true, but never both.
Using
Venn diagrams, you can also see why E and I are contradictory. If E is true (in
either the Boolean or Aristotelian interpretations), area 2 is shaded (i.e.,
empty). But in the I proposition, area 2
has an X (i.e., not empty). Since area 2 is either empty or not, one or
the other, E or I, must be true, but never both.
The Modern Square of Opposition
There’s
not much to the modern square of opposition – just the two pairs of
contradictories.
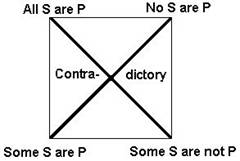
The Modern
|
|
Contradictories |
|
A
is true |
O
is false |
|
E
is true |
I
is false |
|
I
is true |
E
is false |
|
O
is true |
A
is false |
|
A
is false |
O
is true |
|
E
is false |
I
is true |
|
I
is false |
E
is true |
|
O
is false |
A
is true |
The Traditional
Your
textbook shows the traditional square of opposition. Here are a few alternative depictions. Use
whatever you find useful.
1. From Lander
University (philosophy.lander.edu/logic/square.html)

2. From Wikipedia
(http://en.wikipedia.org/wiki/Square_of_opposition)
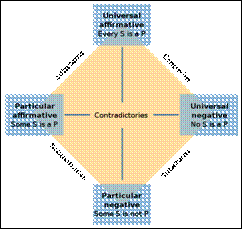
3.
The Traditional
|
|
Contradictories |
Contraries
(A and E) |
Subcontraries
(I and O) |
Subalternation |
|
A
is true |
False
O |
False
E |
N/A |
I
is true |
|
E
is true |
False
I |
False
A |
N/A |
O
is true |
|
I
is true |
False
E |
N/A |
U
– both subcontraries may be T |
N/A |
|
O
is true |
False
A |
N/A |
U
– both subcontraries may be T |
N/A |
|
A
is false |
True
O |
U
– both contraries may be F |
N/A |
N/A |
|
E
is false |
True
I |
U
– both contraries may be F |
N/A |
N/A |
|
I
is false |
True
E |
N/A |
O
is true |
A
is false |
|
O
is false |
True
A |
N/A |
I
is true |
E
is false |
Contraries
The
contrary relationship holds between A and E in the traditional (Aristotelian)
interpretation ONLY.
Two
statements are contraries of each other if
·
if
one is true, the other is false
BUT
·
If
one is false, the other’s truth value is undetermined (both statement might be
false).
In
categorical logic, there is one pair of contraries: A and E in the traditional interpretation only
In
the modern (Boolean) square of opposition, there is no contrary relationship
between any two categoricals.
Using
the traditional Aristotelian Venn diagrams, here’s why A and E are
contraries. Look closely at the diagrams
for traditional A and E above.
If
the traditional A proposition is true, then, area 2 is non-empty, which means
that E (which claims area 2 is empty) must be false. Likewise, if the traditional E is true, area
1 is non-empty, which means A must be false.
Thus if A is true, E is false, and if E is true, A is false.
Why
might both be false? We can easily think of examples that demonstrate the
possibility that an A and an E can both be false. For example, “All WVC students are female”
(an A proposition) is false, and so is “No WVC students are female” (an E
proposition).
A
and E are NOT contraries in the Boolean interpretation, however, since the
Boolean A diagram shades area 1 only, and the Boolean E diagram shades area 2
only. The diagram for A contains no information
about area 2, and the diagram for E contains no information about area 1.
Subcontraries
Two
statements are subcontraries of each other if
·
if
one is false, the other is true
BUT
·
If
one is true, the other’s truth value is undetermined (both statement might be
true).
In
categorical logic, there is one pair of subcontraries: I and
O in the traditional interpretation only
In
the modern square of opposition, there is no subcontrary relationship between
any two categoricals.
Using
Venn diagrams, here’s why I and O are subcontraries in the Aristotelian
interpretation:
The
Venn diagram for the I statement (in both the traditional and modern sesnses)
says area 2 is non-empty (has an X) – something exists here.
The
Venn diagram for the O statement (in both the traditional and modern sesnses)
says area 1 is non-empty (has an X) – something exists here.
Since
the Aristotelian interpretation assumes that Ss exist; of course, that’s what
makes the traditional interpretation different from the modern one. Thus any
individual S must be either in P or not in P, and one or the other of the
diagrams (I or O) must be correct for any S. Furthermore, if more than one S
exists, it is possible some might be P AND some non-P. In either case – whether
there is only one S or more than one – areas
1 and 2 are never both empty, i.e., either area 1 is non-empty or 2 is
non-empty (or both).
I
and O are NOT subcontraries in the Boolean interpretation, however. The Boolean interpretation does not assume
the existence of Ss. If we don’t assume the existence of Ss, both area 1 and
area 2 could be empty. In the Boolean interpretation, when we put an X in area
1 or 2, we’re claiming that Ss exist.
Subalternation
The
subalternation relationship is a relationship of implication, i.e., it concerns
a couple of pairs of arguments, where
we ask whether the conclusion must be true if
the premise is true.
The
relationships in these arguments are not commutative;
validity only works in one direction, from premise to conclusion.
Pair
1 Subalterns (same quality, with true universal premise to true particular
conclusion):
(1) Premise: A (2) Premise: E
Conclusion: I Conclusion: O
Assuming
the same quality, in the Pair 1 subalternations, the premise is always the
universal; the conclusion is always the particular.
Pair
1 subalternation arguments are valid in the traditional interpretation as long
as Ss exist. If the argument has the
subalternation form but Ss don’t exist, we say the argument is invalid because it contains the existential fallacy.
Pair
2 Subalterns (same quality, with false
particular premise to false universal conclusion):
(1) Premise: I is false (2)
Premise: O is false.
Conclusion: A is false. Conclusion: E is
false.
Assuming
the same quality, in the Pair 2 subalternations, the premise is always the
negation of the particular; the conclusion is always the negation of the
universal. Again, these arguments are valid in the Aristotelian interpretation
as long as Ss exist. Here’s why.
Consider
argument (1) of the second pair of subalterns: false I implies false A. By the
contradictory relationship (which holds for both Boolean and Aristotelian
views), if I is false, E is true. And in
the Aristotelian view, since E and A are contraries, if E is true, A must be
false!
Consider
argument (2) of the second pair of subalterns: false O implies false E. By the
contradictory relationship (which holds for both Boolean and Aristotelian
views), if O is false, A is true. And in
the Aristotelian view, since E and A are contraries, if A is true, E must be
false.
Sandy's X10 Host Home Page | Sandy's Google Sites Home Page
Questions or comments? sandy_lafave@yahoo.com